1.二阶行列式的几何意义

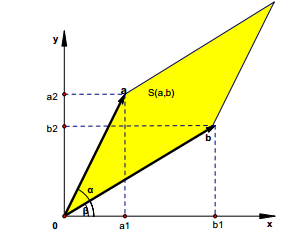
就是由行列式的向量所张成的平行四边形的面积。

也等于二维向量叉乘的数值

\begin{aligned} &\mathrm{D}=\left|\begin{array}{l} \mathrm{a}_1, \mathrm{a}_2 \\ b_1, b_2 \end{array}\right|\\ &\mathbf{a}=\left(\begin{array}{ll} a_1 & a_2 \end{array}\right), \quad \mathbf{b}=\left(\begin{array}{ll} b_1 & b_2 \end{array}\right) \end{aligned}

行列式的定义与展开

2.三阶行列式的几何意义

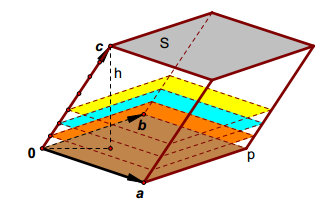
一个 ​3 \times 3 阶的行列式是其行向量或列向量所张成的平行六面体的有向体积。
行列式的定义与展开

3.行列式的空间缩放意义

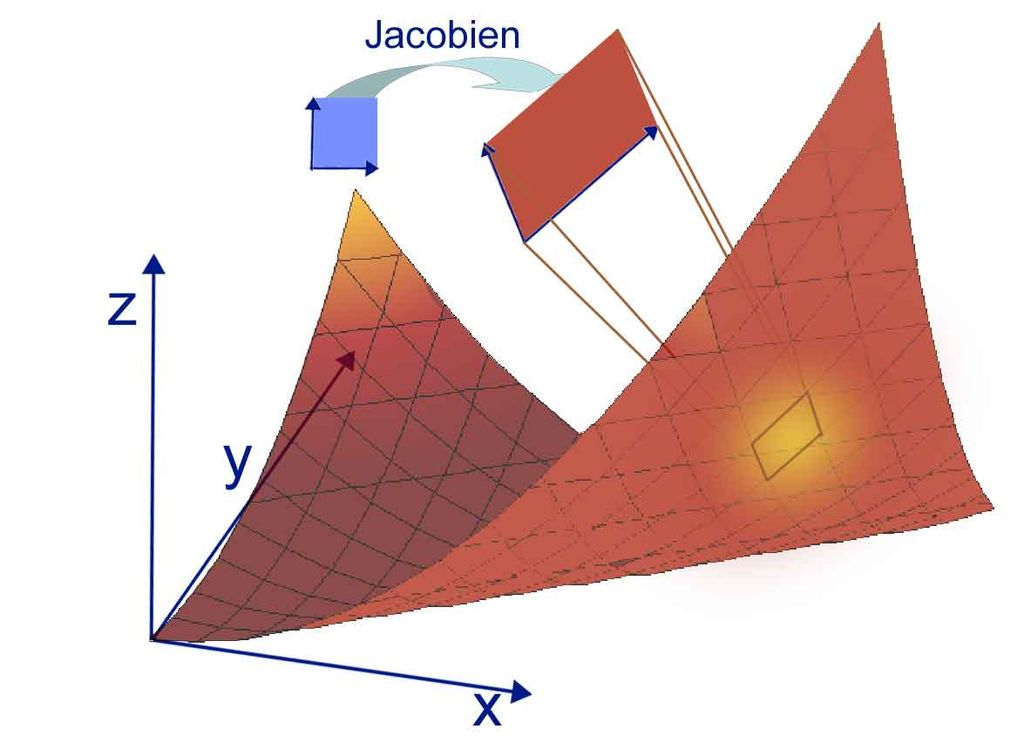
行列式体现了线性变换对于空间体积（二维、三维或n维）的缩放作用，雅可比行列式是把一个体积元（蓝色）变换成另一个（红色）时两者的体积之比
行列式的定义与展开|225

4.行列式化为对角形的几何解释：
\left|\begin{array}{ll} a_1 & a_2 \\ b_1 & b_2 \end{array}\right|=\left|\begin{array}{cc} a_1 & 0 \\ 0 & \frac{a_1 b_2-a_2 b_1}{a_1} \end{array}\right|

一个二阶行列式所表示的平行四边形被变成了一个对角行列式所表示的正（长）方形。
三阶行列式有类似的变换情形，对角化的过程会把一个平行六面体变化为一个等体积的立方体或长方体。
那么阶行列式我们亦不怀疑的认为也可以被表示成一个维的长方体的几何图形。

5.行列式与特征值的几何联系

首先介绍特征值和特征向量的几何和物理意义
摘自《线性代数的几何意义》
我们知道，矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。
若 ​\boldsymbol{A} 是 ​n 阶矩阵,且 ​\boldsymbol{A} 的特征值为 ​\lambda_1, \lambda_2, \cdots, \lambda_n, 则 ​|\boldsymbol{A}|=\lambda_1 \lambda_2 \cdots \lambda_n.
由（3）可知，行列式体现了对空间体积元的缩放比例，特征向量可以看成矩阵对应缩放空间的基(只有线性伸缩)，特征值则表示在对应基方向上的缩放系数，因此体积元整体缩放系数等于各基上缩放系数乘积（类似长方体体积公式）。